Introduction et présentation
La ville de Lyon compte environ 45 ponts. Celui de la Guillotière est situé sur le Rhône entre le pont Wilson et le pont de l’Université. Il fait la jonction entre le cours Gambetta et la rue de la Barre [Figure 1].


Il fait partie des ponts ou le tablier est une poutre en acier comportant trois travées et dont la principale, située au centre, possède une portée de 88 mètres pour une longueur totale d’environ 205 mètres. Ces travées sont en appui sur deux piles en béton immergées dans le Rhône et deux culées situées sur chaque rive [Figure 1,2 et 3].
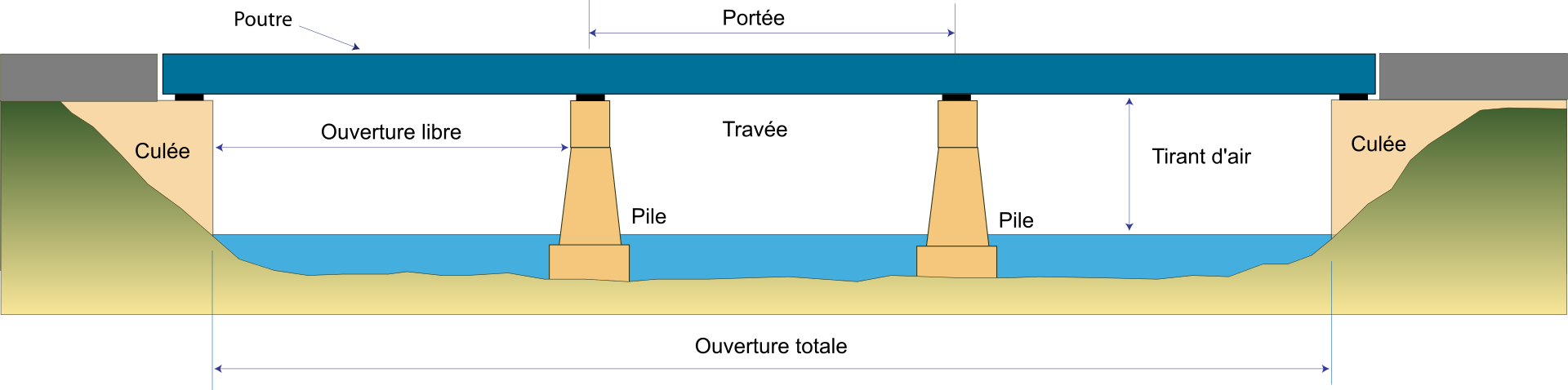
D’un point de vue mécanique, ce pont travaille essentiellement en flexion et est prévu pour des portées situées entre 5 mètres et 300 mètres [Figure 4]. Son comportement élastique fera l’objet de la partie 2.
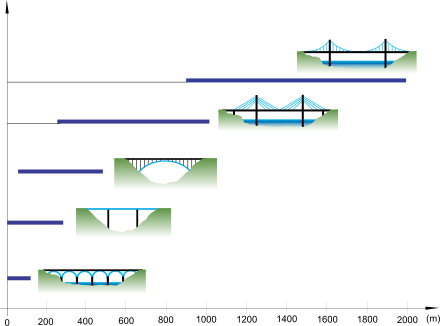
Élasticité du pont de la Guillotière
Afin de modéliser le pont simplement, en première approximation on considèrera que les trois travées sont d’une longueur identique de 88 mètres. Ce qui permettra d’utiliser les symétries pour faciliter les calculs des efforts tranchants et des moments fléchissants. D’autre part, du fait que la poutre soit en appui en quatre points, la structure est hyperstatique d’ordre 2.

La section du tablier peut être considérée comme un rectangle de largueur 0,3 mètre et de hauteur 0,07 mètre [Source 1]. On considèrera que le revêtement du pont possède un poids volumique de 25 kilos newtons par mètre cube [Source 2]. Ces hypothèses permettent de considérer une densité linéique de charge « p » égale à 525 newtons par mètre. On obtient ainsi après des calculs de résistance de matériaux les diagrammes des efforts tranchants « T » [Figure 6] :
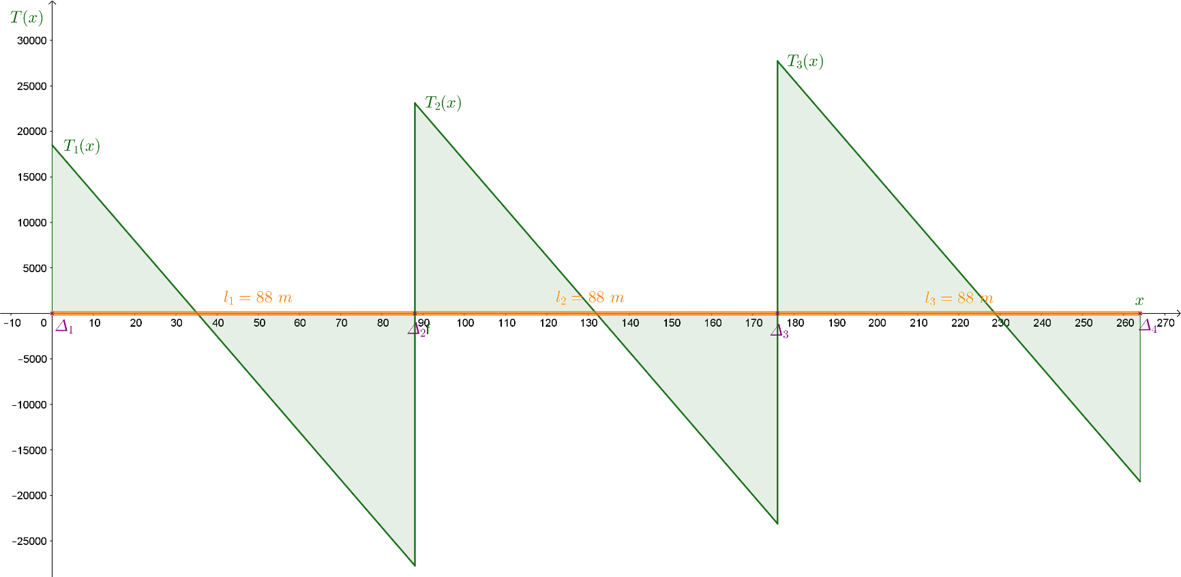
Sur ce diagramme on peut observer que les deux zones du pont les plus contraintes en termes d’efforts tranchants sont les extrémités de la travée centrale, ou l’amplitude des efforts et de l’ordre d’environ 50820 newtons. Cette amplitude correspond à une charge de 5,18 tonnes. Cette valeur admissible n’est bien entendu pas exacte car pour l’obtenir nous avons effectué beaucoup d’hypothèses approximatives. Elle permet cependant d’avoir un ordre de grandeur suffisant pour se représenter l’intensité des efforts que peuvent supporter un tel pont.
A titre indicatif les trois efforts tranchants obtenus par le calcul sont :
T1(x)=18480−525x, 0≤x≤88T2(x)=69300−525x, 88≤x≤175T3(x)=120120−525x, 176≤x≤264T_1 (x)=18480-525x , \ 0≤x≤88 \\ T_2 (x)=69300-525x ,\ 88≤x≤175 \\ T_3 (x)=120120-525x ,\ 176≤x≤264T1(x)=18480−525x, 0≤x≤88T2(x)=69300−525x, 88≤x≤175T3(x)=120120−525x, 176≤x≤264
De la même manière il est possible d’obtenir le diagramme des moments fléchissants « Mf » [Figure 7] :
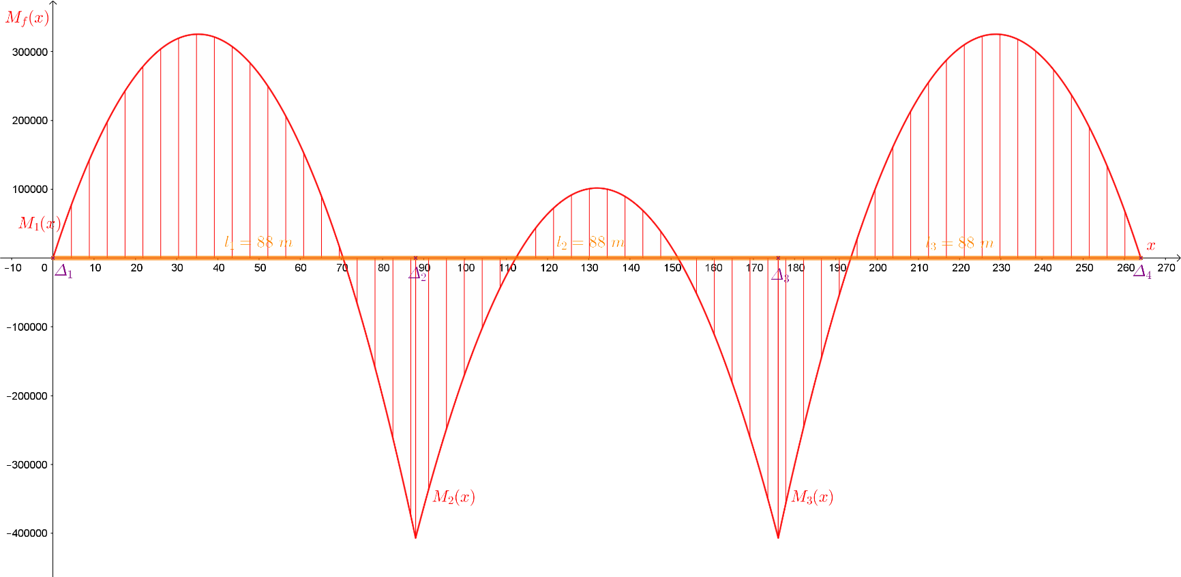
Comme pour les efforts tranchants, les moments fléchissants sont plus importants au niveau des extrémités de la travée centrale.
A titre indicatif les trois moments fléchissants obtenus par le calcul sont :
M1(x)=18480x−262.5x2, 0≤x≤88M2(x)=69300x−262.5x2−4472160, 88≤x≤175M3(x)=120120x−262.5x2−13416480, 176≤x≤264M_1 (x)=18480x-262.5x^2 ,\ 0≤x≤88 \\ M_2 (x)=69300x-262.5x^2-4472160 ,\ 88≤x≤175 \\ M_3 (x)=120120x-262.5x^2-13416480 ,\ 176≤x≤264M1(x)=18480x−262.5x2, 0≤x≤88M2(x)=69300x−262.5x2−4472160, 88≤x≤175M3(x)=120120x−262.5x2−13416480, 176≤x≤264
Conclusions
Comme on a pu l’observer sur les diagrammes des figures 6 et 7. Le pont est le plus contraint sur les zones extrêmes de la travée centrale. Ce qui est intéressant c’est de remarquer que les efforts tranchants dérivent des moments fléchissants.
Évidement le pont est dimensionné pour résister à de tels efforts et très souvent on applique aussi un coefficient de sécurité pour être large. Cependant cette étude seule ne suffit pas pour construire un pont. Il y a bien d’autres aspects à prendre en compte ! Par exemple les sollicitations extérieures au pont, comme l’écoulement de l’eau. Ou encore le frottement de l’air sur les surfaces du pont. Ou bien encore la réponse vibratoire du pont au passage de nombreux véhicules…
Et voilà, merci d’être arrivé au bout de votre lecture. J’espère que celle-ci a su attiser votre curiosité. On se retrouve bientôt pour un autre article ! ! !




